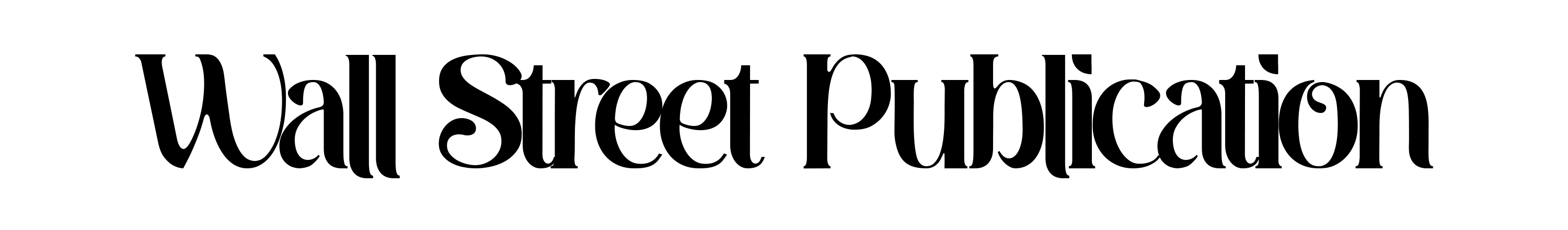The unique model of this story appeared in Quanta Journal.
Since their discovery in 1982, unique supplies often known as quasicrystals have bedeviled physicists and chemists. Their atoms prepare themselves into chains of pentagons, decagons, and different shapes to type patterns that by no means fairly repeat. These patterns appear to defy bodily legal guidelines and instinct. How can atoms presumably “know” easy methods to type elaborate nonrepeating preparations with out a sophisticated understanding of arithmetic?
“Quasicrystals are one of those things that as a materials scientist, when you first learn about them, you’re like, ‘That’s crazy,’” mentioned Wenhao Solar, a supplies scientist on the College of Michigan.
Just lately, although, a spate of outcomes has peeled again a few of their secrets and techniques. In a single research, Solar and collaborators tailored a technique for learning crystals to find out that at the least some quasicrystals are thermodynamically secure—their atoms received’t settle right into a lower-energy association. This discovering helps clarify how and why quasicrystals type. A second research has yielded a brand new technique to engineer quasicrystals and observe them within the means of forming. And a 3rd analysis group has logged beforehand unknown properties of those uncommon supplies.
Traditionally, quasicrystals have been difficult to create and characterize.
“There’s no doubt that they have interesting properties,” mentioned Sharon Glotzer, a computational physicist who can be based mostly on the College of Michigan however was not concerned with this work. “But being able to make them in bulk, to scale them up, at an industrial level—[that] hasn’t felt possible, but I think that this will start to show us how to do it reproducibly.”
Vikram Gavini, Sambit Das, Woohyeon Baek, Wenhao Solar, and Shibo Tan maintain examples of geometric shapes that seem in quasicrystals. The College of Michigan researchers have proven that at the least some quasicrystals are thermodynamically secure.
{Photograph}: Marcin Szczepanski Michigan Engineering‘Forbidden’ Symmetries
Practically a decade earlier than the Israeli physicist Dan Shechtman found the primary examples of quasicrystals within the lab, the British mathematical physicist Roger Penrose thought up the “quasiperiodic”—virtually however not fairly repeating—patterns that may manifest in these supplies.
Penrose developed units of tiles that might cowl an infinite airplane with no gaps or overlaps, in patterns that don’t, and can’t, repeat. In contrast to tessellations manufactured from triangles, rectangles, and hexagons—shapes which can be symmetric throughout two, three, 4 or six axes, and which tile house in periodic patterns—Penrose tilings have “forbidden” fivefold symmetry. The tiles type pentagonal preparations, but pentagons can’t match snugly facet by facet to tile the airplane. So, whereas the tiles align alongside 5 axes and tessellate endlessly, totally different sections of the sample solely look comparable; precise repetition is inconceivable. Penrose’s quasiperiodic tilings made the duvet of Scientific American in 1977, 5 years earlier than they made the leap from pure arithmetic to the actual world.